Introdução a trigonometria

Trigonometria

Relações no triângulo retângulo

Para entender as relações trigonométricas dentro de um triângulo retângulo é necessário saber, primeiro, o que é essa figura. Imagine um retângulo dividido em dois pela diagonal.

Você terá dois triângulos retângulos. Daí o nome. É o triângulo que possui um ângulo igual a 90º (ângulo reto).

Ao pé da letra, trigonometria quer dizer as relações de medidas de triângulos nos triângulos retângulos. Mas existem também relações trigonométricas em outros tipos de triângulos e em outras figuras geométricas.

Elementos de um triângulo retângulo

O triângulo retângulo é formado por catetos e hipotenusa:

Você terá dois triângulos retângulos. Daí o nome. É o triângulo que possui um ângulo igual a 90º (ângulo reto).

Ao pé da letra, trigonometria quer dizer as relações de medidas de triângulos nos triângulos retângulos. Mas existem também relações trigonométricas em outros tipos de triângulos e em outras figuras geométricas.

Elementos de um triângulo retângulo

O triângulo retângulo é formado por catetos e hipotenusa:

Sendo  o ângulo reto, o lado oposto tem o nome de hipotenusa ( ) e os dois outros lados ( e ) são chamados de catetos.

Definição das relações trigonométricas

Vamos definir as medidas dos lados do triângulo retângulo usando letras. A medida do cateto será c (medida do lado oposto ao ângulo C), a do cateto será b (oposto ao ângulo B) e finalmente a hipotenusa (oposto ao ângulo Â) será a.
O seno do ângulo B será a medida do cateto oposto sobre a medida da hipotenusa:

O co-seno será a medida do cateto adjacente sobre a medida da hipotenusa:

A tangente será a medida do cateto oposto sobre o cateto adjacente:

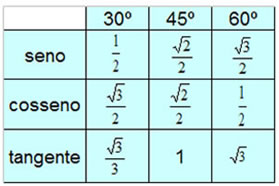
Ângulos notáveis

Para obter o seno, o co-seno e a tangente dos ângulos 30º, 45º e 60º, construa a seguinte tabela:

X	0o	30o	45o	60o
sen x
cos x

Na linha dos senos escreva os números de 1 a 3 e na dos co-senos de 3 a 1:

X	30o	45o	60o
sen x	1	2	3
cos x	3	2	1

Tire a raiz quadrada de cada um:

X	30o	45o	60o
sen x
cos x

Divida tudo por 2:

X	30o	45o	60o
sen x
cos x

Simplifique, pois, logo:

X	30o	45o	60o
sen x
cos x

Como a tangente de um ângulo é a razão entre o seno e o co-seno

Você pode deduzir os valores das tangentes dividindo o seno pelo co-seno. O resultado será a tabela a seguir:
Seno, co-seno e tangente de ângulos notáveis:

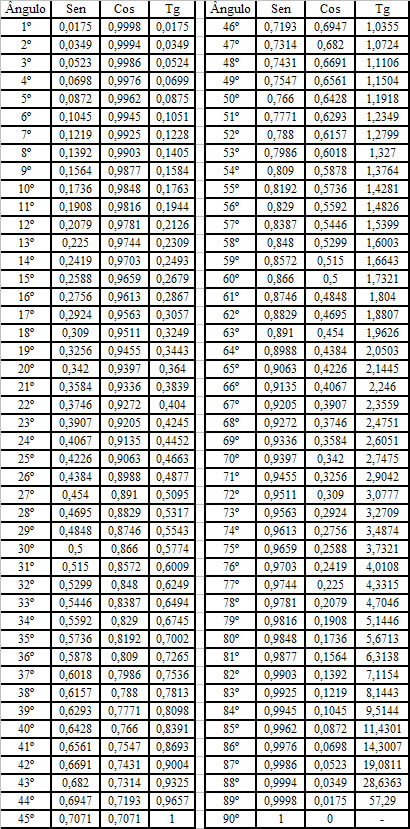
 Tabela completa: